my_brush = circular_brush(7)
my_brush = notched_square_brush(5, 1)
show_mask(my_brush)No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)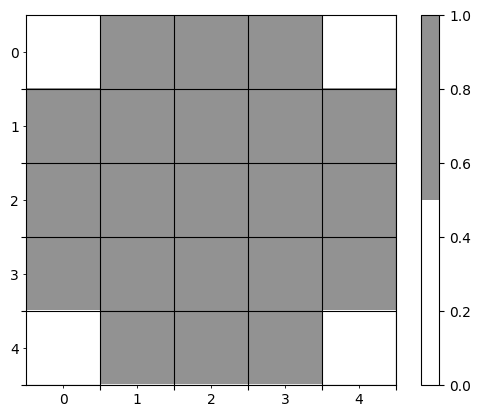
No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
It’s not very well explained in the paper what the latent design actually is. In this case we’ll just assume it’s an array of the same shape as the design, but with continuous values between 0 and 1.
new_latent_design (shape, bias=0, r=None, r_scale=1)
The transform removes some of the noise from the latent design.
transform (latent, brush, beta=5.0)
conditional_algirithm_step (latent_t, design, brush, verbose=False)
conditional_generator (latent_t, brush, verbose=False)
generate_feasible_design (latent_t, brush, verbose=False, backend='auto')
| Type | Default | Details | |
|---|---|---|---|
| latent_t | |||
| brush | |||
| verbose | bool | False | |
| backend | str | auto | backend: ‘auto’, ‘rust’, ‘python’ |
latent_t = transform(latent, my_brush)
plt.imshow(latent_t, cmap="Greys", vmin=-1, vmax=1)
plt.colorbar()
plt.show()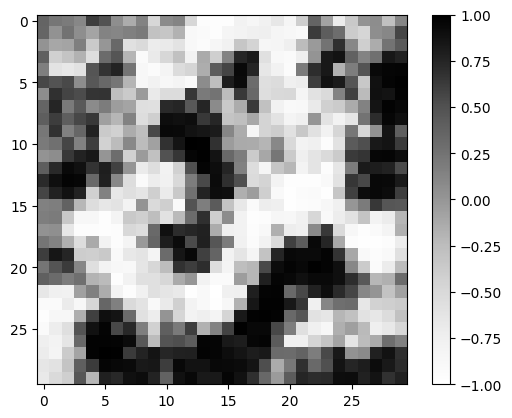
In practice however, it’s probably more useful to generate a design mask straight away (+1.0 for solid, -1.0 for void):
generate_feasible_design_mask_ (latent_t, brush, backend='auto')
We cannot just call jax.grad on our feasible design mask generator. All gradients will be zero as our mask generator is not differentiable…
Moreover, if we would have chosen the Rust-based backend, the above cell would have errored out…
In stead, we use a straight-through estimator (a.k.a. identity function) for our feasible design:
generate_feasible_design_mask (latent_t, brush)
generate_feasible_design_mask_jvp (primals, tangents)